高中数学第二数学归纳法试题

已知数列{a_n}的前n项和S_n，a₁=﹣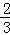，S_n+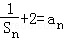（n≥2）．
（1）计算S₁，S₂，S₃，猜想S_n的表达式并用数学归纳法证明；
（2）设b_n=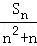，数列的{b_n}的前n项和为T_n，求证：T_n＞﹣．

观察下列式子：，，，…，
根据上述规律，第个不等式应该为 ．

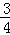设函数其中是的导函数．
（1）令，猜测的表达式并给予证明；
（2）若恒成立，求实数的取值范围；
（3）设，比较与的大小，并说明理由．

数列满足，前n项和．
（1）写出；
（2）猜出的表达式，并用数学归纳法证明．

用数学归纳法证明：时，由到左边需要添加的项是（）

A．	B．
C．	D．

用数学归纳法证明不等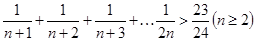的过程中，由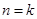递推到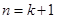时，不等式左边（）

A．增加了一项

B．增加了一项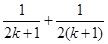

C．增加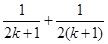了，又减少了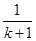

D．增加了，又减少了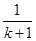

给出以下数阵，按各数排列规律，则的值为（ ）

A．

B．

C．

D．326

数学归纳法证明成立时，从到左边需增加的乘积因式是（）

A．

B．

C．

D．

用数学归纳法证明：“”．从“到”左端需增乘的代数式为（）

A．	B．
C．	D．

用数学归纳法证明：

用数学归纳法证明“”时，由的假设证明时，如果从等式左边证明右边，则必须证得右边为（）

A．

B．

C．

D．

利用数学归纳法证明“”，在验证成立时，等号左边是（）

A．

B．

C．

D．

用数学归纳法证明（n＋1）（n＋2）…（n＋n）＝2ⁿ·1·3…（2n－1）（n∈N^*）时，从“n＝k到n＝k＋1”左边需增乘的代数式为（ ）

A．2k＋1

B．2（2k＋1）

C．

D．

（本小题满分14分）设数列的前项和为，且对任意的都有，
（1）求数列的前三项；
（2）猜想数列的通项公式，并用数学归纳法证明；
（3）求证：对任意都有．

观察下面算式：
；
；
；
；
…………
，其中，那么____________.