如图9所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题: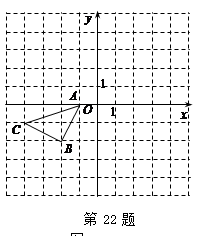
(1)分别写出点A、B两点的坐标;
(2)作出△ABC关于坐标原点成中心对称的△A1B1C1;
(3)作出点C关于是x轴的对称点P. 若点P向右平移x个单位长度后落在△A1B1C1的内部,请直接写出x的取值范围.
相关知识点
推荐套卷
如图9所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题: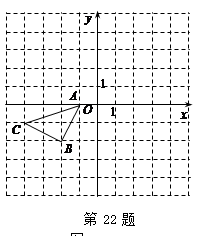
(1)分别写出点A、B两点的坐标;
(2)作出△ABC关于坐标原点成中心对称的△A1B1C1;
(3)作出点C关于是x轴的对称点P. 若点P向右平移x个单位长度后落在△A1B1C1的内部,请直接写出x的取值范围.