（1）探究新知：如图1，已知△ABC与△ABD的面积相等， 试判断AB与CD的位置关系，并说明理由．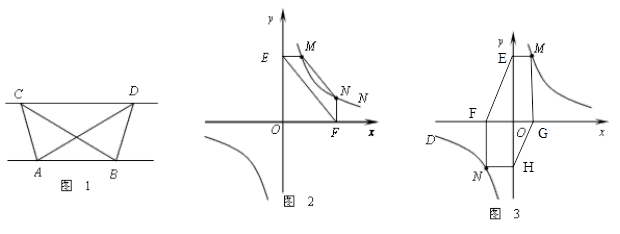 
（2）结论应用：如图2，点M，N在反比例函数
（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F． 试证明：MN∥EF．
（3）变式探究：如图3，点M，N在反比例函数（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，过点M作MG⊥x轴，过点N作NH⊥y轴，垂足分别为E、F、G、H． 试证明：EF ∥GH．
推荐套卷
（1）探究新知：如图1，已知△ABC与△ABD的面积相等， 试判断AB与CD的位置关系，并说明理由．
（2）结论应用：如图2，点M，N在反比例函数（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F． 试证明：MN∥EF．
（3）变式探究：如图3，点M，N在反比例函数（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，过点M作MG⊥x轴，过点N作NH⊥y轴，垂足分别为E、F、G、H． 试证明：EF ∥GH．
粤公网安备 44130202000953号