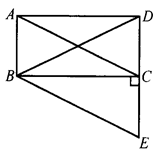
数学课上,李老师出示了这样一道题目:如图,正方形 的边长为
的边长为 ,
, 为边
为边 延长线上的一点,
延长线上的一点,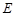 为
为 的中点,
的中点, 的垂直平分线交边
的垂直平分线交边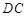 于
于 ,交边
,交边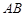 的延长线于
的延长线于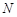 .当
.当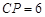 时,
时, 与
与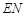 的比值是多少?
的比值是多少?
经过思考,小明展示了一种正确的解题思路:过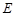 作直线平行于
作直线平行于 交
交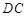 ,
,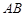 分别于
分别于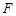 ,
,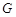 ,如图
,如图 ,则可得:
,则可得: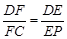 ,因为
,因为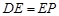 ,所以
,所以 .可求出
.可求出 和
和 的值,进而可求得
的值,进而可求得 与
与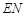 的比值.
的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了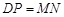 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
相关知识点
推荐套卷
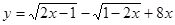 ,求
,求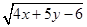 的平方根.
的平方根.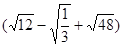 ÷
÷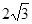
 粤公网安备 44130202000953号
粤公网安备 44130202000953号