阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为
,
,
,记
,那么三角形的面积为
. ①
古希腊几何学家海伦
,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约
约
,曾提出利用三角形的三边求面积的秦九韶公式:
. ②
下面我们对公式②进行变形:
.
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦
秦九韶公式.
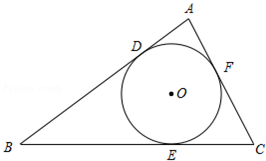
问题:如图,在
中,
,
,
,
内切于
,切点分别是
、
、
.
(1)求
的面积;
(2)求
的半径.