如图1,△ABD和△BDC都是边长为1的等边三角形。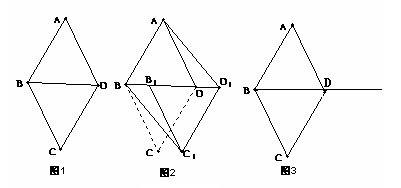
(1)四边形ABCD是菱形吗?为什么?
(2)如图2,将△BDC沿射线BD方向平移到△B1D1C1的位置,则四边形ABC1D1 是平行四边形吗?为什么?
(3)在△BDC移动过程中,四边形ABC1D1有可能是矩形吗?如果是,请求出点B移动的距离(写出过程);如果不是,请说明理由(图3供操作时使用)。
相关知识点
推荐套卷
如图1,△ABD和△BDC都是边长为1的等边三角形。
(1)四边形ABCD是菱形吗?为什么?
(2)如图2,将△BDC沿射线BD方向平移到△B1D1C1的位置,则四边形ABC1D1 是平行四边形吗?为什么?
(3)在△BDC移动过程中,四边形ABC1D1有可能是矩形吗?如果是,请求出点B移动的距离(写出过程);如果不是,请说明理由(图3供操作时使用)。