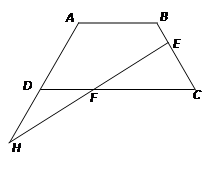已知：如图，在梯形ABCD中，AB∥CD，AD＝BC，AB＝10，CD＝18，∠ADC＝60°，过BC上一点E作直线EH，交CD于点F，交AD的延长线于点H，且EF＝FH．
（1）求梯形ABCD的面积；
（2）求证：AD＝DH＋BE．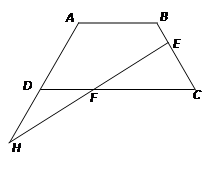
相关试题
中，BE、CF分别平分
和
，
于E，
于F，求证：EF//BC
相关知识点
推荐套卷
已知：如图，在梯形ABCD中，AB∥CD，AD＝BC，AB＝10，CD＝18，∠ADC＝60°，过BC上一点E作直线EH，交CD于点F，交AD的延长线于点H，且EF＝FH．
（1）求梯形ABCD的面积；
（2）求证：AD＝DH＋BE．
粤公网安备 44130202000953号