已知三棱锥P－ABC中，PA⊥平面ABC，AB⊥AC，PA=AC=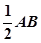
，N为AB上一点，AB=4AN， M,S分别为PB,BC的中点.
（Ⅰ）证明：CM⊥SN；
（Ⅱ）求SN与平面CMN所成角的大小.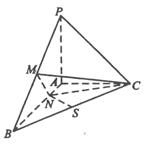
是圆的直径，
垂直圆所在的平面，
是圆上任一点，
平面
．
中，
，
，
，
，
分别为
，
和对角线
的中点．求证：平面
平面
．
平面
，求证：过
有且只有一个平面
．
中，
分别是
上的点，且直线
与
交于点
，求证
三点共线．
的底面边长和各侧棱长都是13，
分别是
上的点且
．求证：直线
平面
相关知识点
推荐套卷
已知三棱锥P－ABC中，PA⊥平面ABC，AB⊥AC，PA=AC=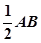，N为AB上一点，AB=4AN， M,S分别为PB,BC的中点.
（Ⅰ）证明：CM⊥SN；
（Ⅱ）求SN与平面CMN所成角的大小.
粤公网安备 44130202000953号