（本小题满分16分）
已知椭圆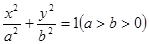
的左、右顶点分别A、B，椭圆过点（0，1）且离心率
.
（1）求椭圆的标准方程；
（2）过椭圆上异于A，B两点的任意一点P作PH⊥
轴，H为垂足，延长HP到点Q，且PQ=HP，过点B作直线
轴，连结AQ并延长交直线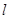
于点M，N为MB的中点，试判断直线QN与以AB为直径的圆O的位置关系.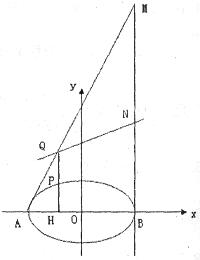
相关试题
的分布列及数学期望E
–
，平面
⊥平面
=
=
=2．
；
与平面
中，
，
，
，
．
平面
；
是棱
的中点，在棱
上是否存在一点
，使
平面
.
、
的值；
的值.推荐套卷
（本小题满分16分）
已知椭圆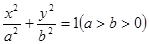的左、右顶点分别A、B，椭圆过点（0，1）且离心率.
（1）求椭圆的标准方程；
（2）过椭圆上异于A，B两点的任意一点P作PH⊥轴，H为垂足，延长HP到点Q，且PQ=HP，过点B作直线轴，连结AQ并延长交直线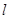于点M，N为MB的中点，试判断直线QN与以AB为直径的圆O的位置关系.
粤公网安备 44130202000953号