如图,△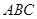 是等边三角形,点
是等边三角形,点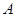 坐标为(-8,0)、点
坐标为(-8,0)、点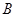 坐标为(8,0),点
坐标为(8,0),点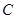 在
在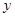 轴的正半轴上.一条动直线从
轴的正半轴上.一条动直线从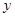 轴出发,以每秒1个单位长度的速度沿
轴出发,以每秒1个单位长度的速度沿 轴向右平移,直线与直线
轴向右平移,直线与直线 交于点
交于点 ,与线段
,与线段 交于点
交于点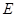 .以
.以 为边向左侧作等边△
为边向左侧作等边△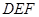 ,
,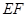 与
与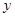 轴的交点为
轴的交点为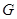 .当点
.当点 与点
与点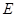 重合时,直线停止运动,设直线的运动时间为(秒).
重合时,直线停止运动,设直线的运动时间为(秒).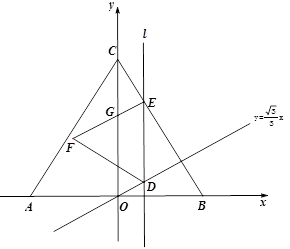
(1)填空:点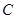 的坐标为 ,四边形
的坐标为 ,四边形 的形状一定是 ;
的形状一定是 ;
(2)试探究:四边形 能不能是菱形?若能,求出相应的的值;若不能,请说明理由.
能不能是菱形?若能,求出相应的的值;若不能,请说明理由.
(3)当t为何值时,点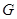 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙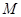 上?并求出此时⊙
上?并求出此时⊙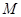 的半径.
的半径.
相关知识点
推荐套卷
 时,求AF及BE的长.
时,求AF及BE的长.

 的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
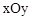 中,一次函数
中,一次函数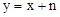 和反比例函数
和反比例函数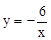 的图象都经过点
的图象都经过点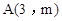 .
.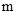 的值和一次函数的表达式;
的值和一次函数的表达式;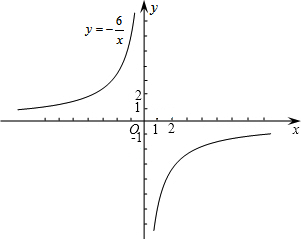
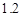 倍,求:甲、乙两班各有多少名学生.
倍,求:甲、乙两班各有多少名学生. 粤公网安备 44130202000953号
粤公网安备 44130202000953号