 两地相距45千米,图中折线表示某骑车人离
两地相距45千米,图中折线表示某骑车人离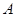 地的距离
地的距离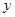 与时间
与时间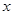 的函数关系.有一辆客车9点从
的函数关系.有一辆客车9点从 地出发,以45千米/时的速度匀速行驶,并往返于
地出发,以45千米/时的速度匀速行驶,并往返于 两地之间.(乘客上、下车停留时间忽略不计)
两地之间.(乘客上、下车停留时间忽略不计) 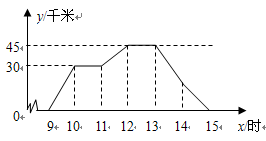
(1)从折线图可以看出,骑车人一共休息 次,共休息 小时;
(2)请在图中画出9点至15点之间客车与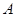 地距离
地距离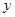 随时间
随时间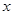 变化的函数图象;
变化的函数图象;
(3)通过计算说明,何时骑车人与客车第二次相遇.
相关知识点
推荐套卷
 两地相距45千米,图中折线表示某骑车人离
两地相距45千米,图中折线表示某骑车人离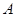 地的距离
地的距离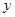 与时间
与时间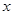 的函数关系.有一辆客车9点从
的函数关系.有一辆客车9点从 地出发,以45千米/时的速度匀速行驶,并往返于
地出发,以45千米/时的速度匀速行驶,并往返于 两地之间.(乘客上、下车停留时间忽略不计)
两地之间.(乘客上、下车停留时间忽略不计) 
(1)从折线图可以看出,骑车人一共休息 次,共休息 小时;
(2)请在图中画出9点至15点之间客车与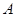 地距离
地距离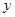 随时间
随时间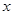 变化的函数图象;
变化的函数图象;
(3)通过计算说明,何时骑车人与客车第二次相遇.