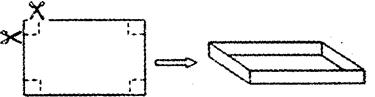
如图,把…张长10cm,宽8cm的矩形硬纸枥的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
你感到折合而成的长方体盒子的侧面积(不含底面)会不会有最大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由
相关知识点
推荐套卷
如图,把…张长10cm,宽8cm的矩形硬纸枥的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
你感到折合而成的长方体盒子的侧面积(不含底面)会不会有最大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由
