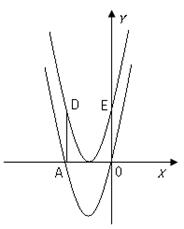
如图,抛物线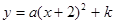 与x轴交于A,0两点,将抛物线向上移动4个单位长度后得到一条新抛物线,它的顶点在x轴上,新抛物线上的D,E两点分别是A,O两点平移后的对应点。设两条抛物线、线段AD和线段OE围成的面积为S。P(m,n)是新抛物线上一个动点,切满足
与x轴交于A,0两点,将抛物线向上移动4个单位长度后得到一条新抛物线,它的顶点在x轴上,新抛物线上的D,E两点分别是A,O两点平移后的对应点。设两条抛物线、线段AD和线段OE围成的面积为S。P(m,n)是新抛物线上一个动点,切满足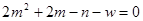
⑴求新抛物线的解析式。
⑵当m=-2时,点F的坐标为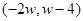 ,试判断直线DF与AE的位置关系,并说明理由。
,试判断直线DF与AE的位置关系,并说明理由。
⑶当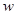 的值最小时,求△AEP的面积与S的数量关系。
的值最小时,求△AEP的面积与S的数量关系。
相关知识点
推荐套卷
如图,抛物线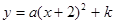 与x轴交于A,0两点,将抛物线向上移动4个单位长度后得到一条新抛物线,它的顶点在x轴上,新抛物线上的D,E两点分别是A,O两点平移后的对应点。设两条抛物线、线段AD和线段OE围成的面积为S。P(m,n)是新抛物线上一个动点,切满足
与x轴交于A,0两点,将抛物线向上移动4个单位长度后得到一条新抛物线,它的顶点在x轴上,新抛物线上的D,E两点分别是A,O两点平移后的对应点。设两条抛物线、线段AD和线段OE围成的面积为S。P(m,n)是新抛物线上一个动点,切满足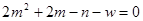

⑴求新抛物线的解析式。
⑵当m=-2时,点F的坐标为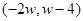 ,试判断直线DF与AE的位置关系,并说明理由。
,试判断直线DF与AE的位置关系,并说明理由。
⑶当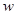 的值最小时,求△AEP的面积与S的数量关系。
的值最小时,求△AEP的面积与S的数量关系。