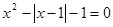先阅读下面的例题:
解方程:
解:(1)当x≥0时,原方程化为
解得x1=2,x2=-1(不合题意,舍去)
(2)当x<0时,原方程化为
解得x1=-2,x2=1(不合题意,舍去)
所以原方程的解是x1=2,x2=-2
请参考以上例题的解法
解方程: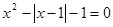
相关知识点
推荐套卷
先阅读下面的例题:
解方程:
解:(1)当x≥0时,原方程化为
解得x1=2,x2=-1(不合题意,舍去)
(2)当x<0时,原方程化为
解得x1=-2,x2=1(不合题意,舍去)
所以原方程的解是x1=2,x2=-2
请参考以上例题的解法
解方程: