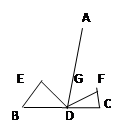如图,在△ABC中,E、F分别是AB、AC上的点。
①AD平分∠BAC;②DE⊥AB,DF⊥AC;③AD⊥EF以其中的两个为条件,另一个为结论,可构成三个命题,即⑴①②→③;⑵①③→②;⑶②③→①
(1)试判断上述三个命题是否正确。(直接作答)
(2)请证明你认为正确的命题。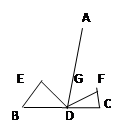
相关知识点
推荐套卷
如图,在△ABC中,E、F分别是AB、AC上的点。
①AD平分∠BAC;②DE⊥AB,DF⊥AC;③AD⊥EF以其中的两个为条件,另一个为结论,可构成三个命题,即⑴①②→③;⑵①③→②;⑶②③→①
(1)试判断上述三个命题是否正确。(直接作答)
(2)请证明你认为正确的命题。