已知:如图1,在平面直角坐标系中,O为坐标原点,直线y=kx+b与x轴、y轴分别交与点A、B,与双曲线y=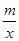 相交于C、D两点,且点D的坐标为(1,6).
相交于C、D两点,且点D的坐标为(1,6).
(1)当点C的横坐标为2时,试求直线AB的解析式,并直接写出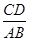 的值为 .
的值为 .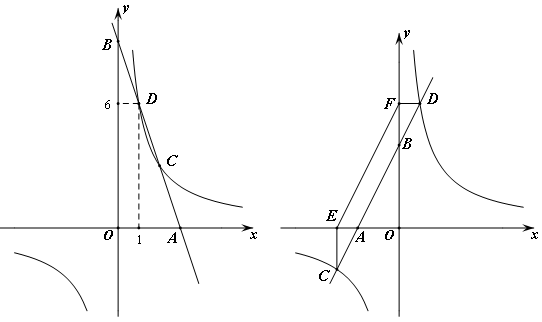
(2)如图2,当点A落在x 轴的负半轴时,过点C作x轴的垂线,垂足为E,过点D作y轴的垂线,垂足为F,连接EF.①判断ΔEFC的面积和ΔEFD的面积是否相等,并说明理由;②当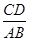 =2时,求tan∠OAB的值.
=2时,求tan∠OAB的值.
推荐套卷
已知:如图1,在平面直角坐标系中,O为坐标原点,直线y=kx+b与x轴、y轴分别交与点A、B,与双曲线y=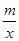 相交于C、D两点,且点D的坐标为(1,6).
相交于C、D两点,且点D的坐标为(1,6).
(1)当点C的横坐标为2时,试求直线AB的解析式,并直接写出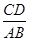 的值为 .
的值为 .
(2)如图2,当点A落在x 轴的负半轴时,过点C作x轴的垂线,垂足为E,过点D作y轴的垂线,垂足为F,连接EF.①判断ΔEFC的面积和ΔEFD的面积是否相等,并说明理由;②当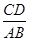 =2时,求tan∠OAB的值.
=2时,求tan∠OAB的值.