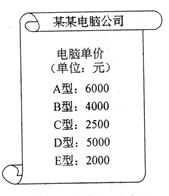
某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑,希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑。
写出所有选购方案(利用树状图或列表法表示)。
如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
现知希望中学购甲、乙两种电脑共36台,(价格如图所示),恰好用了10万元人民币,其中购买的甲品牌电脑为A型号电脑,求购买的A型号的电脑有几台?
相关知识点
推荐套卷

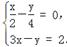
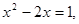 求
求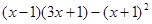 的值
的值

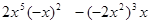
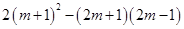

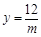 ,要使△DEF为等腰三角形,m的值应为多少?
,要使△DEF为等腰三角形,m的值应为多少? 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
的取值情况进行分析,说明按哪种优惠方法购买比较便宜; 粤公网安备 44130202000953号
粤公网安备 44130202000953号