设函数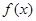
是定义在［－1，0）∪（0，1］上的奇函数，当x∈［－1，0）时，
（a∈R).
（1）当x∈(0，1］时，求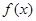的解析式；
（2）若a＞－1，试判断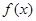在（0，1）上的单调性，并证明你的结论；
（3）是否存在a，使得当x∈（0，1）时，f(x)有最大值－6.
相关试题
+
+…+
<
.
+
≥a+b.
+lg
+lg
>lga+lgb+lgc.推荐套卷
设函数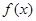是定义在［－1，0）∪（0，1］上的奇函数，当x∈［－1，0）时，（a∈R).
（1）当x∈(0，1］时，求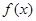的解析式；
（2）若a＞－1，试判断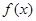在（0，1）上的单调性，并证明你的结论；
（3）是否存在a，使得当x∈（0，1）时，f(x)有最大值－6.
粤公网安备 44130202000953号