平面直角坐标系中，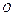
为坐标原点，给定两点A（1，0）、B（0，－2），点C满足
其中
、
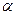且
．
（Ⅰ）求点C的轨迹方程；
（Ⅱ）设点C的轨迹与双曲线
交于两点M、N，且以MN为直径的圆过原点，求证：
为定值．
相关知识点
推荐套卷
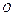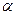平面直角坐标系中，为坐标原点，给定两点A（1，0）、B（0，－2），点C满足其中、且．
（Ⅰ）求点C的轨迹方程；
（Ⅱ）设点C的轨迹与双曲线交于两点M、N，且以MN为直径的圆过原点，求证：为定值．
粤公网安备 44130202000953号