如图，在平面直角坐标系中，已知三个点A(1，3)，B(3，1)，O(0，0)．求△ABO的面积；
将△ABO向左平移4个单位长度，向下平移1个单位长度，得到△DEF，其中A，B，O分
别对应点D，E，F，请在图中画出△DEF,并写出D、E、F的坐标．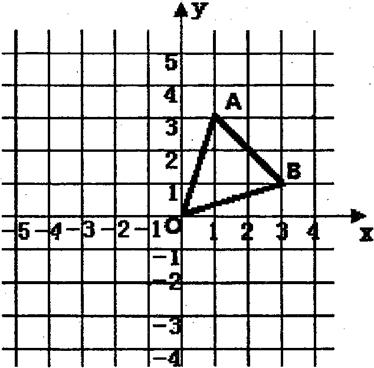
；
，
，
，比较a、b、c的大小．
，求
的值.
，
，求
的值.
.相关知识点
推荐套卷
如图，在平面直角坐标系中，已知三个点A(1，3)，B(3，1)，O(0，0)．求△ABO的面积；
将△ABO向左平移4个单位长度，向下平移1个单位长度，得到△DEF，其中A，B，O分
别对应点D，E，F，请在图中画出△DEF,并写出D、E、F的坐标．
粤公网安备 44130202000953号