如图，在平面直角坐标系中，点A、B分别在x轴y轴的正半轴上，线段OA的长是不等式5x﹣4＜3（x+2）的最大整数解，线段OB的长是一元二次方程x2﹣2x﹣3=0的一个根，将Rt△ABO沿BE折叠，使AB边落在OB边所在的y轴上，点A与点D重合．
（1）求OA、OB的长；
（2）求直线BE的解析式；
（3）在平面内是否存在点M，使B、O、E、M为顶点的四边形为平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．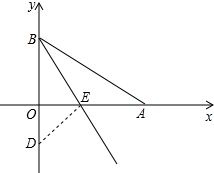
如图，在平面直角坐标系中，点A、B分别在x轴y轴的正半轴上，线段OA的长是不等式5x﹣4＜3（x+2）的最大整数解，线段OB的长是一元二次方程x2﹣2x﹣3=0的一个根，将Rt△ABO沿BE折叠，使AB边落在OB边所在的y轴上，点A与点D重合．
（1）求OA、OB的长；
（2）求直线BE的解析式；
（3）在平面内是否存在点M，使B、O、E、M为顶点的四边形为平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
……
.
，其中x=-
”，小强做题时把“x=-
，其中x=1．
粤公网安备 44130202000953号