如图，等腰Rt△ABD中，AB=AD，点M 为边AD上一动点，点E在DA的延长线上，且AM=AE，以BE为直角边，向外作等腰Rt△BEG，MG交AB于N，连NE、DN．
（1）求证：∠BEN=∠BGN．
（2）求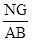
的值．
（3）当M在AD上运动时，探究四边形BDNG的形状，并证明之．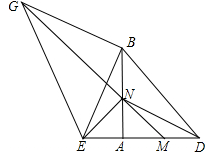
如图，等腰Rt△ABD中，AB=AD，点M 为边AD上一动点，点E在DA的延长线上，且AM=AE，以BE为直角边，向外作等腰Rt△BEG，MG交AB于N，连NE、DN．
（1）求证：∠BEN=∠BGN．
（2）求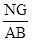的值．
（3）当M在AD上运动时，探究四边形BDNG的形状，并证明之．
；
；
；
粤公网安备 44130202000953号