已知圆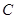 过点
过点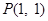 ,且与圆
,且与圆 关于直线
关于直线 对称.
对称.
(1)求圆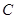 的方程;
的方程;
(2)设 为圆
为圆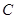 上一个动点,求
上一个动点,求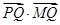 的最小值;
的最小值;
(3)过点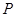 作两条相异直线分别与圆
作两条相异直线分别与圆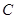 相交于
相交于 ,且直线
,且直线 和
和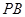 直线的倾斜角互补,
直线的倾斜角互补,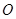 为坐标原点,试判断直线
为坐标原点,试判断直线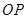 和
和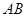 是否平行,并说明理由.
是否平行,并说明理由.
相关知识点
推荐套卷
已知圆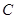 过点
过点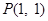 ,且与圆
,且与圆 关于直线
关于直线 对称.
对称.
(1)求圆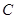 的方程;
的方程;
(2)设 为圆
为圆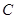 上一个动点,求
上一个动点,求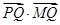 的最小值;
的最小值;
(3)过点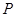 作两条相异直线分别与圆
作两条相异直线分别与圆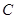 相交于
相交于 ,且直线
,且直线 和
和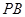 直线的倾斜角互补,
直线的倾斜角互补,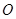 为坐标原点,试判断直线
为坐标原点,试判断直线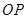 和
和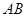 是否平行,并说明理由.
是否平行,并说明理由.