如图6，已知动圆M过定点F（1,0）且与x轴相切，点F 关于圆心M 的对称点为 F'，动点F’的轨迹为C．
（1）求曲线C的方程；
（2）设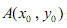
是曲线C上的一个定点，过点A任意作两条倾斜角互补的直线，分别与曲线C相交于另外两点P 、Q．
①证明：直线PQ的斜率为定值；
②记曲线C位于P 、Q两点之间的那一段为l．若点B在l上，且点B到直线PQ的
距离最大，求点B的坐标．
相关试题
＋(m2＋2m－3)i，当m为何值时．
＋(m2－5m－6)i(m∈R)，试求实数m分别取什么值时，z分别为：
sinx，sinx)，b＝(cosx，sinx)，x∈
.相关知识点
推荐套卷
如图6，已知动圆M过定点F（1,0）且与x轴相切，点F 关于圆心M 的对称点为 F'，动点F’的轨迹为C．
（1）求曲线C的方程；
（2）设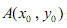是曲线C上的一个定点，过点A任意作两条倾斜角互补的直线，分别与曲线C相交于另外两点P 、Q．
①证明：直线PQ的斜率为定值；
②记曲线C位于P 、Q两点之间的那一段为l．若点B在l上，且点B到直线PQ的
距离最大，求点B的坐标．
粤公网安备 44130202000953号