某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如图所示（在答题卡上）.
（Ⅰ）请先求出频率分布表中①、②位置相应的数据，再在答题纸上完成下列频率分布直方图；
（Ⅱ）为了能选拔出最优秀的学生，该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？
（Ⅲ）在（2）的前提下，学校决定在6名学生中随机抽取2名学生接受A考官的面试，求第四组至少有一名学生被考官A面试的概率？
相关试题
从4名男生,3名女生中选出三名代表：
(1)不同的选法共有多少种?
(2)至少有一名女生的不同的选法共有多少种?
(3)代表中男、女生都要有的不同的选法共有多少种?
,
,
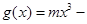
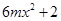
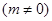在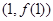
处的切线方程为
.
的值；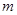
，使得对任意的
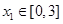，总存在
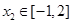，使得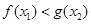
成立？若存在，求出实数
.
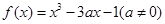求
的单调区间； 
若
处取得极值，直线y=
与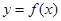
的图象有三个不同的交点，求
.
在
处有极值，求
；
上为增函数，求
(单位：千克)与销售价格
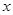(单位：元/千克)满足关系式
，其中
，
为常数，已知销售价格为5元/千克时，每日可售出该商品11千克．相关知识点
推荐套卷
粤公网安备 44130202000953号