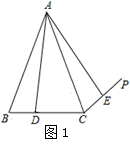
某校把一块沿河的三角形废地(如图)开辟为生物园,已知∠ACB=90°,
∠CAB=54°,BC=60米.现学校准备从点C处向河岸AB修一条小路CD,使得CD将生物园分割成面积相等的两部分.请你用直尺和圆规在图中作出小路CD(保留作图痕迹);
为便于浇灌,学校在点C处建了一个蓄水池,利用管道从河中取水.已知每铺设1米管道费用为50元,求铺设管道的最低费用.(sin36°≈0.588,cos36°≈0.809,tan36°≈0.727,精确到1元)

相关知识点
推荐套卷
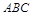 中,
中, ,现在△
,现在△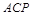 =∠
=∠ ,在
,在 上取一点
上取一点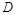 ,在
,在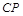 上取一点
上取一点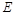 ,使
,使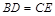 ,并连接
,并连接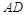 ,
,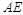 .
.
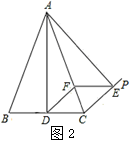
 ;
; =144°,求∠
=144°,求∠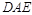 的度数;
的度数;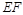 ∥
∥ 于点
于点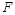 ,连接
,连接 .试判断四边形
.试判断四边形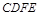 的形状,并
的形状,并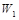 、
、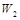 、
、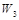 、
、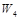 表示)、化学4题(用
表示)、化学4题(用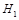 、
、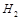 、
、 、
、 表示)、生物2题(用
表示)、生物2题(用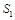 、
、 表示),共10题. 某校为备战实验操作考试,对学生进行模拟训练.由学生在每科测试时抽签选定一个进行实验操作.若学生测试时,第一次抽签选定物理实验题,第二次抽签选定化学实验题,第三次抽签选定生物实验题.已知王强同学抽到的物理实验题为
表示),共10题. 某校为备战实验操作考试,对学生进行模拟训练.由学生在每科测试时抽签选定一个进行实验操作.若学生测试时,第一次抽签选定物理实验题,第二次抽签选定化学实验题,第三次抽签选定生物实验题.已知王强同学抽到的物理实验题为 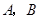 两处,用仪器探测生命迹象
两处,用仪器探测生命迹象 ,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(参考数据:
,已知探测线与地面的夹角分别是30°和60°(如图),求该生命迹象所在位置的深度(参考数据: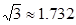 ,结果保留一位小数).
,结果保留一位小数).
 和格点O.
和格点O.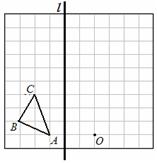
 ;
; ;
; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号