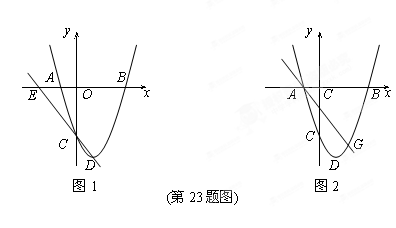
如图1,在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a>0)的图像顶点为D,与y轴交于点C,与x轴交于点A、B,点A在原点的左侧,点B的坐标为(3,0),OB=OC,tan∠ACO=.求这个二次函数的解析式;
若平行于x轴的直线与该抛物线交于点M、N,且以MN为直径的圆与x轴相切,求该圆的半径长度;Com]
如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上的一动点,当点P运动到什么位置时,△AGP的面积最大?求此时点P的坐标和△AGP的最大面积.

相关知识点
推荐套卷
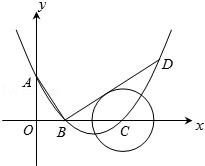
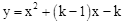 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.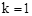 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;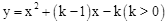 与x轴交于C,D两点(点C在点D的左侧).在直线
与x轴交于C,D两点(点C在点D的左侧).在直线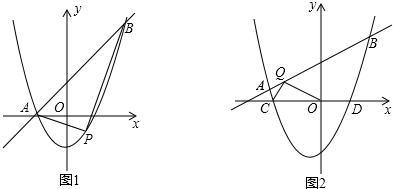
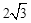 ).将矩形OABC绕点O逆时针旋转30°,得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段GF、GH、GO和x轴于点M、P、N、D,连结MH.
).将矩形OABC绕点O逆时针旋转30°,得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段GF、GH、GO和x轴于点M、P、N、D,连结MH.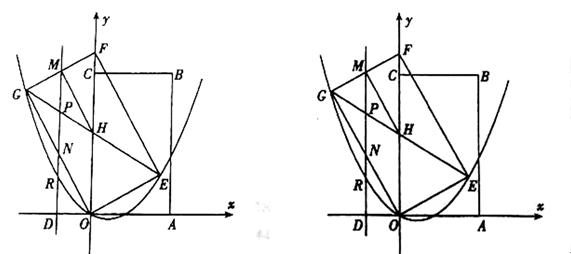
 经过G、O、E三点,则它的解析式为: ;
经过G、O、E三点,则它的解析式为: ;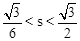 时,确定点Q的横坐标的取值范围.
时,确定点Q的横坐标的取值范围. 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).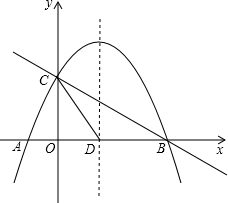
 ,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。
,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。
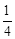 ,当a=2时,求T的值;
,当a=2时,求T的值; 粤公网安备 44130202000953号
粤公网安备 44130202000953号