汕头二中拟建一座长
米，宽
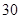米的长方形体育馆．按照建筑要求，每隔
米（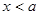
，
为正常数）需打建一个桩位，每个桩位需花费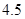
万元（桩位视为一点且打在长方形的边上），桩位之间的米墙面需花
万元，在不计地板和天花板的情况下，当为何值时，所需总费用最少？
相关试题
中，前5项和前10项的和分别为25和100。数列
中，
。
、
；
，求
。
。
的值；
，求
和
。
的各项均为正实数，且其前
项和
满足
。（1）证明：数列
，求数列
的前
。
所对的分别是
。已知
。（1）求
的值；
的值。
是等比数列
的公比
且
项的和。若
。（1）求数列
，求数列
的前
。推荐套卷
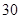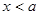汕头二中拟建一座长米，宽米的长方形体育馆．按照建筑要求，每隔米（，为正常数）需打建一个桩位，每个桩位需花费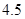万元（桩位视为一点且打在长方形的边上），桩位之间的米墙面需花万元，在不计地板和天花板的情况下，当为何值时，所需总费用最少？
粤公网安备 44130202000953号