某公司向市场投放三种新型产品，经调查发现第一种产品受欢迎的概率为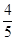
，第二、第三种产品受欢迎的概率分别为
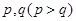，且不同种产品是否受欢迎相互独立.记
为公司向市场投放三种新型产品受欢迎的数量，其分布列为
 |
（Ⅰ）求该公司至少有一种产品受欢迎的概率；
（Ⅱ）求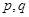
的值；
（Ⅲ）求数学期望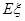
.
相关试题
,
为何实数
总为增函数;
的图象；
，集合
，
，
、
；
是集合A的子集，求实数k的取值范围.
的值．
的值.
相关知识点
推荐套卷
某公司向市场投放三种新型产品，经调查发现第一种产品受欢迎的概率为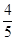，第二、第三种产品受欢迎的概率分别为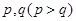，且不同种产品是否受欢迎相互独立.记为公司向市场投放三种新型产品受欢迎的数量，其分布列为
|
（Ⅰ）求该公司至少有一种产品受欢迎的概率；
（Ⅱ）求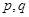的值；
（Ⅲ）求数学期望.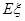
粤公网安备 44130202000953号