如图,四棱锥S—ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB
(Ⅰ)证明:平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小 .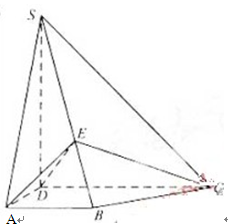
推荐套卷
如图,四棱锥S—ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB
(Ⅰ)证明:平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小 .