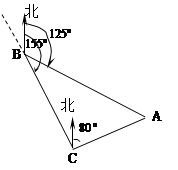如图，货轮在海上以50海里/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155o的方向航行．为了确定船位，在B点处观测到灯塔A的方位角为125o．半小时后，货轮到达C点处，观测到灯塔A的方位角为80o．求此时货轮与灯塔之间的距离（得数保留最简根号）.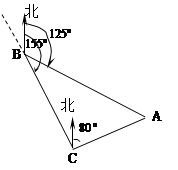
的值；
的值．
,
是同一平面内的两个向量，其中
，
且
与
垂直，(1)求
；
为锐角，若
试求
的值.
；
的大小,并证明
证明你的结论。
相关知识点
推荐套卷
如图，货轮在海上以50海里/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155o的方向航行．为了确定船位，在B点处观测到灯塔A的方位角为125o．半小时后，货轮到达C点处，观测到灯塔A的方位角为80o．求此时货轮与灯塔之间的距离（得数保留最简根号）.
粤公网安备 44130202000953号