从甲、乙两题中选做一题,如果两题都做,只以甲题计分.甲题:若关于x的一元二次方程
 有实数根α、β.求实数k的取值范围;设
有实数根α、β.求实数k的取值范围;设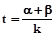 ,求t的最小值.
,求t的最小值.乙题:如图,在△ABC 中,点O是AC边上的一个动点,过点O作直
线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
相关知识点
推荐套卷
从甲、乙两题中选做一题,如果两题都做,只以甲题计分.甲题:若关于x的一元二次方程
 有实数根α、β.求实数k的取值范围;设
有实数根α、β.求实数k的取值范围;设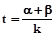 ,求t的最小值.
,求t的最小值.乙题:如图,在△ABC 中,点O是AC边上的一个动点,过点O作直
线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.当点O运动到何处时,四边形AECF是矩形?并证明你的结论.