[四川]2012届四川省沐川县初三二调考试数学卷
如图,∠1=15°,OC⊥OA,点B、O、D在同一直线上,则∠2的度数是
(A) 75° (B) 105°
(C) 115° (D) 165°
2009年初甲型H1N1流感在墨西哥暴发并在全球蔓延,我们应通过注意个人卫生加强防范.研究表明,甲型H1N1流感球形病毒细胞的直径约为0.00000156 m,用科学记数法表示这个数是
A.0.156×10 |
B.0.156×10 | C.1.56×10 |
D.1.56×10 |
将平面直角坐标系内某个图形上各点的横坐标都乘以-1,纵坐标不变,所得图形与原图形的关系是
| A.关于x轴对称 | B.关于y轴对称 | C.关于原点对称 | D.两图形重合 |
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离出发地的距离S(千米)和行驶时间t(小时)之间的函数关系的图象如图所示,根据图中提供的信息,下列不符合图象描述的说法是
| A.甲同学比乙同学先出发半小时 |
| B.乙比甲先到达B地 |
| C.乙在行驶过程中没有追上甲 |
| D.甲的行驶速度比乙的行驶速度慢 |

如图,四边形ABCD是矩形,AB:AD = 4:3,把矩形沿直线AC折叠,点B落在点E处,连接DE,则DE:AC =
| A.1:3 | B.3:8 |
| C.8:27 | D.7:25 |

如图,△ABC是直角边长为a的等腰直角三角形,直角边AB是半圆O的直径,半圆O过C点且与半圆O相切,则图中阴影部分的面积是
A. |
B. |
C. |
D. |

如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,则弦AB的长为 cm.
如果m是从1,2,3三个数中任取的一个数,n是从1,2两个数中任取的一个数,那么关于x的一元二次方程 有实数根的概率为 .
有实数根的概率为 .
如图,正方形OABC的面积是4,点B在反比例函数 的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S.则当S=m(m为常数,且0<m<4)时,点R的坐标是_______.(用含m的代数式表示)
的图象上.若点R是该反比例函数图象上异于点B的任意一点,过点R分别作x轴、y轴的垂线,垂足为M、N,从矩形OMRN的面积中减去其与正方形OABC重合部分的面积,记剩余部分的面积为S.则当S=m(m为常数,且0<m<4)时,点R的坐标是_______.(用含m的代数式表示)
如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.求证:△ABE≌△CAD;
求∠BFD的度数.

已知一次函数y=x+2与反比例函数 ,其中一次函数y=x+2的图象经过点P(k,5).
,其中一次函数y=x+2的图象经过点P(k,5).试确定反比例函数的表达式;
若点Q是上述一次函数与反比例函数图象在第三象限的交点,求点Q的坐标.
某校为了了解九年级学生体育测试成绩情况,抽查了一部分学生的体育测试成绩,甲、乙、丙三位同学将抽查出的学生的测试成绩按A、B、C、D四个等级进行统计,并将统计结果绘制成如下统计图,其中测试成绩在90~100分为A级,75~89分为B级, 60~74分为C级,60分以下为D级。甲同学计算出成绩为C的频率是0.2,乙同学计算出成绩为A、B、C的频率之和为0.96,丙同学计算出成绩为A的频数与成绩为B的频数之比
为7:12.结合统计图回答下列问题: 这次抽查了多少人?
所抽查学生体育测试成绩的中位数在哪个等级内?
若该校九年级学生共有500人,请你估计这次体育测试成绩为A级和B级的学生共有多少人?

海船以5海里/小时的速度向正东方向行驶,在A处看见灯塔B在海船的北偏东60°方向,2小时后船行驶到C处,发现此时灯塔B在海船的北偏西45°方向,求此时灯塔B到C处的距离。
某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B的工作效率相同,且都为C队的2倍,若由一个工程队单独完成,C队比A 队要多用10天.学校决定由三个工程队一齐施工,要求至多6天完成维修任务.三个工程队都按原来的工作效率施工2天时,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B队提高的工作效率仍然都是C队提高的2倍.这样他们至少还需要3天才能成整个维修任务.求工程队A原来平均每天维修课桌的张数;
求工程队A提高工作效率后平均每天多维修课桌张数的取值范围.
从甲、乙两题中选做一题,如果两题都做,只以甲题计分.甲题:若关于x的一元二次方程
 有实数根α、β.求实数k的取值范围;设
有实数根α、β.求实数k的取值范围;设 ,求t的最小值.
,求t的最小值.乙题:如图,在△ABC 中,点O是AC边上的一个动点,过点O作直
线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
如图,Rt△ABC内接于⊙O,AC=BC,∠BAC的平分线AD与⊙0交于点D,与BC交于点E,延长BD,与AC的延长线交于点F,连结CD,G是CD的中点,连结0G.判断0G与CD的位置关系,写出你的结论并证明;
求证:AE=BF;
若OG·DE=3(2-
 ),求⊙O的面积.
),求⊙O的面积.



 中,自变量x的取值范围在数轴上可表示为
中,自变量x的取值范围在数轴上可表示为
 的大致图象,那么一次函数
的大致图象,那么一次函数 的图象不经过
的图象不经过
 .
. ,化简:
,化简: ___.
___. , 那么
, 那么 的值等于_____.
的值等于_____.
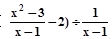 ,其中
,其中 满足
满足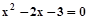 .
. 经过A(1,0),B(0,2)两点,顶点为D.
经过A(1,0),B(0,2)两点,顶点为D. ,顶点为
,顶点为 ,若点N在平移后的抛物线上,且满足△
,若点N在平移后的抛物线上,且满足△ 的面积是△
的面积是△ 面积的2倍,求点N的坐标.
面积的2倍,求点N的坐标.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号