某中学在该校抽取若干名学生对“你认为2010年的北京春节联欢晚会节目如何?”进行问卷调查,整理收集到的数据绘制成如下统计图(图(1)图(2)).
根据统计图(1),图(2)提供的信息,解答下列问题:参加问卷调查的学生有 名;
将统计图(1)中“非常精彩”的条形部分补充完整;
在统计图(2)中,“比较好”部分扇形所对应的圆心角是 度;
若全校共有4500名学生,估计全校认为“非常精彩”的学生有 名.
相关知识点
推荐套卷
 请根据以上信息,解答下列问题:
请根据以上信息,解答下列问题: 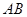 是
是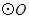 的直径,点
的直径,点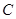 在
在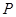 ,
,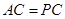 ,
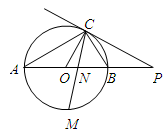
, .
.
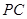 是
是 ;
;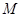 是弧AB的中点,
是弧AB的中点,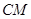 交
交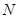 ,若
,若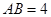 ,求
,求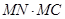 的值.
的值.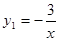 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.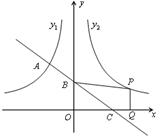
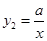 (x>0)的图象与
(x>0)的图象与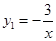 (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在

 粤公网安备 44130202000953号
粤公网安备 44130202000953号