已知数列{an}(n为正整数)是首项为a1,公比为q的等比数列.
(1)求和: ( i ) a1C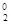 -a2C
-a2C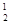 +a3C
+a3C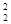 , ( ii ) a1C
, ( ii ) a1C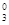 -a2C
-a2C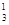 +a3C
+a3C -a4C
-a4C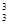 ;
;
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
推荐套卷
已知数列{an}(n为正整数)是首项为a1,公比为q的等比数列.
(1)求和: ( i ) a1C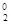 -a2C
-a2C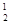 +a3C
+a3C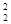 , ( ii ) a1C
, ( ii ) a1C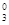 -a2C
-a2C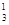 +a3C
+a3C -a4C
-a4C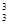 ;
;
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.