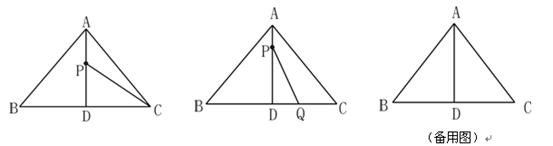
如图，在△ABC中，AB=AC=10厘米，BC=12厘米，AD⊥BC于点D，动点P从点D出发以每秒2厘米的速度在线段AD上向终点A运动．设动点运动时间为t秒．求AD的长．
当△APC的面积为18平方厘米时，求的值．
动点Q从点C出发以每秒1厘米的速度在线段CB上运动．点Q与点P同时出发，且当点P运动到终点A时，点Q也停止运动．是否存在t，使线段PQ把△ADC的面积分为1：2两部分？若存在，请求出t的值；若不存在，请说明理由．
相关试题
（2）班有50名学生，老师安排每人制作一件
型或
型的陶艺品，学校现有甲种制作材料36kg，乙种制作材料29kg，制作，两种型号的陶艺品用料情况如下表：
| 需甲种材料 |
需乙种材料 |
|
| 1件型陶艺品 |
0.9kg |
0.3kg |
| 1件型陶艺品 |
0.4kg |
1kg |
（1）设制作型陶艺品
件，求的取值范围；
（2）请你根据学校现有材料，分别写出七（2）班制作型和型陶艺品的件数．
的解集为a＜x＜b，则a+b的值为多少?
的解集为x＞3，求a的取值范围．
相关知识点
推荐套卷
粤公网安备 44130202000953号