已知,如图,二次函数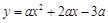
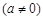 图象的顶点为
图象的顶点为 ,与
,与 轴交于
轴交于 、
、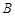 两点(
两点(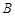 在
在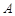 点右侧),点
点右侧),点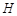 、
、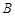 关于直线
关于直线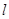 :
: 对称
对称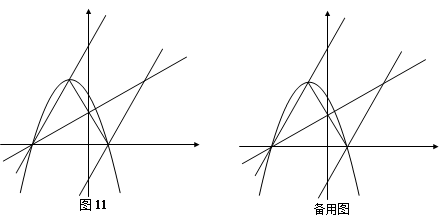
求
 、
、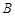 两点坐标,并证明点
两点坐标,并证明点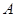 在直线
在直线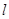 上
上求二次函数解析式;
过点
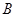 作直线
作直线 ∥
∥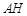 交直线
交直线 于
于 点,
点,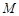 、N分别为直线
、N分别为直线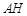 和直线
和直线 上的两个动点,连接
上的两个动点,连接 、
、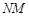 、
、 ,求
,求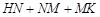 和的最小值.
和的最小值.
相关知识点
推荐套卷
已知,如图,二次函数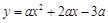
 图象的顶点为
图象的顶点为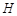 ,与
,与 轴交于
轴交于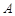 、
、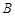 两点(
两点(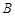 在
在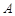 点右侧),点
点右侧),点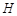 、
、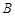 关于直线
关于直线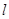 :
: 对称
对称
求
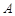 、
、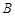 两点坐标,并证明点
两点坐标,并证明点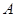 在直线
在直线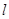 上
上求二次函数解析式;
过点
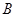 作直线
作直线 ∥
∥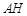 交直线
交直线 于
于 点,
点,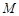 、N分别为直线
、N分别为直线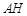 和直线
和直线 上的两个动点,连接
上的两个动点,连接 、
、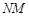 、
、 ,求
,求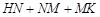 和的最小值.
和的最小值.