如图,C是射线 OE上的一动点,AB是过点 C的弦,直线DA与OE的交点为D,现有三个论断: ①DA是⊙O的切线;②DA=DC;③ OD⊥OB.
请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,
用“★★ ★”表示.并给出证明;我的命题是: .
★”表示.并给出证明;我的命题是: .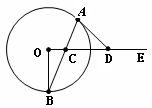
相关知识点
推荐套卷
如图,C是射线 OE上的一动点,AB是过点 C的弦,直线DA与OE的交点为D,现有三个论断: ①DA是⊙O的切线;②DA=DC;③ OD⊥OB.
请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,
用“★★ ★”表示.并给出证明;我的命题是: .
★”表示.并给出证明;我的命题是: .