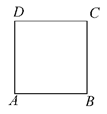
如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进.现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字.质点P从A点出发,规则如下:当正方体上底面出现的数字是1,质点P前进一步(如由A到B);当正方体上底面出现的数字是2,质点P前进两步(如由A到C),当正方体上底面出现的数字是3,质点P前进三步(如由A到D).在质点P转一圈之前连续投掷,若超过一圈,则投掷终止.
(1)求质点P恰好返回到A点的概率;
(2)在质点P转一圈恰能返回到A点的所有结果中,用随机变量ξ表示点P恰能返回到A点的投掷次数,求ξ的数学期望.