目前南昌市正在进行师大地铁站点围挡建设，为缓解北京西路交通压力，计划将该路段实施“交通限行”．在该路段随机抽查了50人，了解公众对“该路段限行”的态度，将调查情况进行整理，制成下表：
（1）完成被调查人员年龄的频率分布直方图；
（2）若从年龄在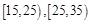
的被调查者中各随机选取两人进行追踪调查，记选中的4人中不赞成“交通限行”的人数为
，求随机变量的分布列和数学期望．
在R上是减函数，求实数
的取值范围。
及直线
．
为何值时，直线与椭圆有公共点？
，求直线的方程．
，离心率为0.6，求椭圆的标准方程。
对一切
恒成立, 求
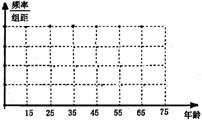
的取值范围。相关知识点
推荐套卷
目前南昌市正在进行师大地铁站点围挡建设，为缓解北京西路交通压力，计划将该路段实施“交通限行”．在该路段随机抽查了50人，了解公众对“该路段限行”的态度，将调查情况进行整理，制成下表：
（1）完成被调查人员年龄的频率分布直方图；
（2）若从年龄在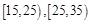的被调查者中各随机选取两人进行追踪调查，记选中的4人中不赞成“交通限行”的人数为，求随机变量的分布列和数学期望．
粤公网安备 44130202000953号