甲乙两队参加奥运知识竞赛,每队三人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为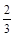
,乙队中三人答对的概率分别为
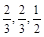,且各人回答得正确与否相互之间没有影响.
(1)若用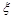
表示甲队的总得分,求随机变量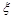分布列和数学期望；
(2)用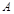
表示事件“甲、乙两队总得分之和为
”,用
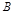表示事件“甲队总得分大于乙队总得分”,求
.
相关试题
|sinx|.
＋b的定义域为
，函数最大值为1，最小值为－5，求a和b的值．
，sin
，－cos
；
与sin
.
＋
；
)－
；
.
的值域和单调区间．相关知识点
推荐套卷
甲乙两队参加奥运知识竞赛,每队三人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为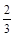,乙队中三人答对的概率分别为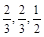,且各人回答得正确与否相互之间没有影响.
(1)若用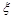表示甲队的总得分,求随机变量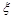分布列和数学期望；
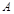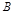(2)用表示事件“甲、乙两队总得分之和为”,用表示事件“甲队总得分大于乙队总得分”,求.
粤公网安备 44130202000953号