如图，已知矩形ABCD是圆柱O1O2的轴截面，N在上底面的圆周O2上，AC、BD相交于点M；
（1）求证：CN⊥平面ADN；
（2）已知圆锥MO1和圆锥MO2的侧面展开图恰好拼成一个半径为2的圆，直线BC与平面CAN所成角的正切值为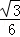
，求异面直线AB与DN所成角的值．
相关试题
中，
，
，
是三角形的三内角，a，b，
是三内角对应的三边长，已知
，求角
是定义在Ｒ上的奇函数，当
时，
，
．
(x≥1)
，求a的取值范围
的取值范围.推荐套卷
如图，已知矩形ABCD是圆柱O1O2的轴截面，N在上底面的圆周O2上，AC、BD相交于点M；
（1）求证：CN⊥平面ADN；
（2）已知圆锥MO1和圆锥MO2的侧面展开图恰好拼成一个半径为2的圆，直线BC与平面CAN所成角的正切值为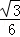，求异面直线AB与DN所成角的值．
粤公网安备 44130202000953号