如图,△ABC中,3条角平分线AE、BD、CF相交于点O,过O点作OG⊥BC垂足为G,
(1)猜想∠BOC与90°+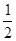 ∠BAC之间的数量关系,并说明理由;
∠BAC之间的数量关系,并说明理由;
(2)∠BOE与∠COG相等吗?为什么?
 |
相关知识点
推荐套卷
如图,△ABC中,3条角平分线AE、BD、CF相交于点O,过O点作OG⊥BC垂足为G,
(1)猜想∠BOC与90°+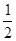 ∠BAC之间的数量关系,并说明理由;
∠BAC之间的数量关系,并说明理由;
(2)∠BOE与∠COG相等吗?为什么?
 |