（本小题满分16分）某商品的市场需求量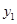
（万件）、市场供应量
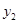（万件）与市场价格x（元/件）分别近似的满足下列关系：
,
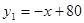，当
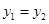时的市场价格称为市场平衡价格，此时的需求量称为平衡需求量。
（1）求平衡价格和平衡需求量；
（2）若要使平衡需求量增加6万件，政府对每件商品应给予多少元补贴？
（3）求当每件商品征税6元时新的平衡价格？
中
，
求证：（1）对角线
⊥平面
。
的外心。
的中点。
（1）求直线
是异面直线，
求证：AD与BC是异面直线。
的三个顶点坐标为分别为：
试判断相关知识点
推荐套卷
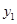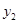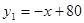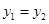（本小题满分16分）某商品的市场需求量（万件）、市场供应量（万件）与市场价格x（元/件）分别近似的满足下列关系：,，当时的市场价格称为市场平衡价格，此时的需求量称为平衡需求量。
（1）求平衡价格和平衡需求量；
（2）若要使平衡需求量增加6万件，政府对每件商品应给予多少元补贴？
（3）求当每件商品征税6元时新的平衡价格？
粤公网安备 44130202000953号