（本小题满分7分）某区拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示．请在答题卷上利用尺规作图作出音乐喷泉M的位置．（要求：不写已知、求作、作法。要写结论，保留作图痕迹，必须先用铅笔再用钢笔或签字笔加真）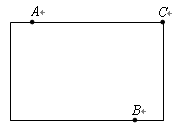
相关试题
（本小题满分7分）某区拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示．请在答题卷上利用尺规作图作出音乐喷泉M的位置．（要求：不写已知、求作、作法。要写结论，保留作图痕迹，必须先用铅笔再用钢笔或签字笔加真）
有两个不相等的实数根．
等边三角形.
(用配方法) （2）3x(x－1)=2－2x
,
，现将△DEF
个单位向右平移，直至E点与C 点重合时停止运动，设运动时
，若存在，试求出CH的值；若不存在，请说明理由．
粤公网安备 44130202000953号