在“传箴言”活动中，某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计，并制成了如下两幅不完整的统计图：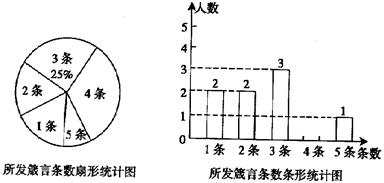
（1）求该班团员在这一个月内所发箴言的平均条数是多少？并将该条形统计图补充完整；
（2）如果发了3条箴言的同学中有两位男同学，发了4条箴言的同学中有三位女同学．现要从发了3条箴言和4条箴言的同学中分别选出一位参加该校团委组织的“箴言”活动总结会，请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．
相关试题
在“传箴言”活动中，某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计，并制成了如下两幅不完整的统计图：
（1）求该班团员在这一个月内所发箴言的平均条数是多少？并将该条形统计图补充完整；
（2）如果发了3条箴言的同学中有两位男同学，发了4条箴言的同学中有三位女同学．现要从发了3条箴言和4条箴言的同学中分别选出一位参加该校团委组织的“箴言”活动总结会，请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．
．已知BC=3，求△ABC平移的距离．
与x轴和y轴的交点坐标．
表示，计算
．某同学做此题时误将
，求得其结果为
，若
，请你帮助他求得正确答案．
粤公网安备 44130202000953号