(满分14分)几何模型:
如图1, 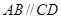 ,O是BD的中点,求证:
,O是BD的中点,求证: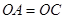 ;
;
模型应用:
(温馨提示:模型应用是指应用模型结论直接解题)
(1)如图2,在梯形ABCD中,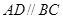 ,点E是腰DC的中点,AE平分
,点E是腰DC的中点,AE平分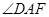 ,求证:AE⊥EF;
,求证:AE⊥EF;
(2)如图3,在⊙O中,AB是⊙O的直径,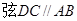 ,点E是OD的中点,点O到AC的距离为1
,点E是OD的中点,点O到AC的距离为1 ,试求阴影部分的面积.
,试求阴影部分的面积. 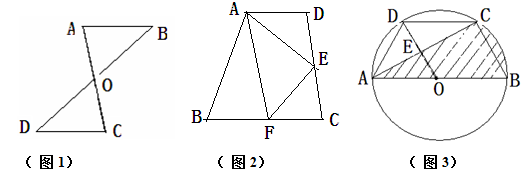
推荐套卷
(满分14分)几何模型:
如图1, 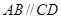 ,O是BD的中点,求证:
,O是BD的中点,求证: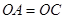 ;
;
模型应用:
(温馨提示:模型应用是指应用模型结论直接解题)
(1)如图2,在梯形ABCD中,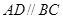 ,点E是腰DC的中点,AE平分
,点E是腰DC的中点,AE平分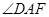 ,求证:AE⊥EF;
,求证:AE⊥EF;
(2)如图3,在⊙O中,AB是⊙O的直径,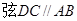 ,点E是OD的中点,点O到AC的距离为1
,点E是OD的中点,点O到AC的距离为1 ,试求阴影部分的面积.
,试求阴影部分的面积. 