(本题满分6分) 探究发散:(1)完成下列填空
①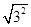 =_____, ②
=_____, ②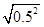 =_____, ③
=_____, ③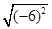 =____,
=____,
④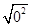 =_____, ⑤
=_____, ⑤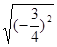 =_____,⑥
=_____,⑥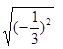 =_____,
=_____,(2)根据计算结果,回答:
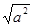 一定等于a吗?你发现其中的规律了吗?请你用自己的语言描述出来:
一定等于a吗?你发现其中的规律了吗?请你用自己的语言描述出来: (3)利用你总结的规律,计算:
①若x<2,则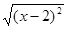 = ; ②
= ; ②
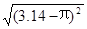 =_____ 。
=_____ 。
(本题满分6分) 探究发散:(1)完成下列填空
①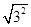 =_____, ②
=_____, ②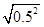 =_____, ③
=_____, ③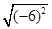 =____,
=____,
④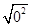 =_____, ⑤
=_____, ⑤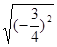 =_____,⑥
=_____,⑥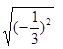 =_____,
=_____,(2)根据计算结果,回答:
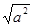 一定等于a吗?你发现其中的规律了吗?请你用自己的语言描述出来:
一定等于a吗?你发现其中的规律了吗?请你用自己的语言描述出来: (3)利用你总结的规律,计算:
①若x<2,则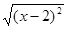 = ; ②
= ; ②
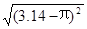 =_____ 。
=_____ 。