(本小题满分14分)如图,单位圆(半径为1的圆)的圆心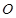 为坐标原点,单位圆与
为坐标原点,单位圆与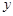 轴的正半轴交与点
轴的正半轴交与点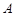 ,与钝角
,与钝角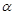 的终边
的终边 交于点
交于点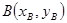 ,设
,设 .
.
(Ⅰ)用 表示
表示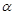 ;
;
(Ⅱ)如果 ,求点
,求点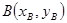 的坐标;
的坐标;
(Ⅲ)求 的最小值.
的最小值.
相关知识点
推荐套卷
(本小题满分14分)如图,单位圆(半径为1的圆)的圆心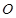 为坐标原点,单位圆与
为坐标原点,单位圆与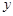 轴的正半轴交与点
轴的正半轴交与点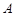 ,与钝角
,与钝角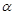 的终边
的终边 交于点
交于点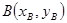 ,设
,设 .
.
(Ⅰ)用 表示
表示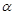 ;
;
(Ⅱ)如果 ,求点
,求点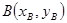 的坐标;
的坐标;
(Ⅲ)求 的最小值.
的最小值.