(普通班)已知椭圆 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆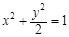 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求k的取值范围.
(实验班)已知函数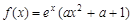
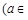 R).
R).
(Ⅰ)若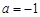 ,求曲线
,求曲线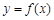 在点
在点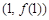 处的的切线方程;
处的的切线方程;
(Ⅱ)若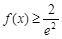 对任意
对任意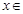
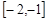 恒成立,求实数
恒成立,求实数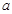 的取值范围.
的取值范围.
推荐套卷
(普通班)已知椭圆 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆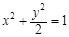 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求k的取值范围.
(实验班)已知函数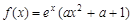
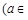 R).
R).
(Ⅰ)若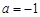 ,求曲线
,求曲线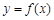 在点
在点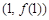 处的的切线方程;
处的的切线方程;
(Ⅱ)若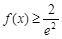 对任意
对任意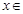
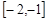 恒成立,求实数
恒成立,求实数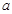 的取值范围.
的取值范围.